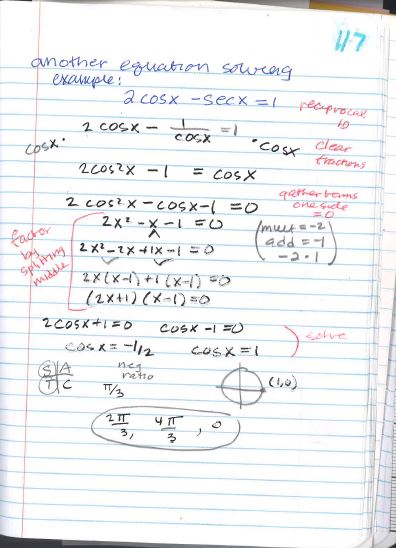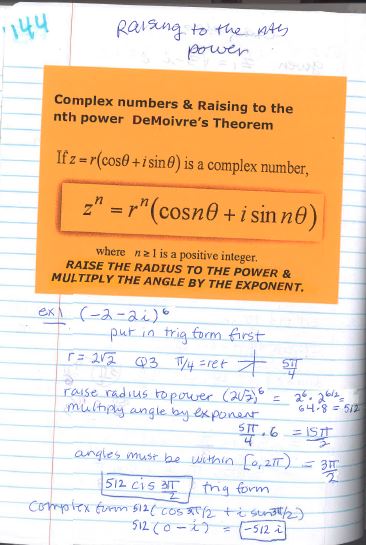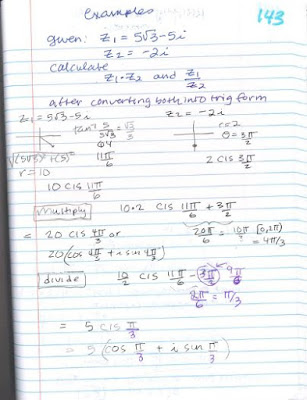I find that my students have a very difficult time with solving trigonometric equations. Part of this stems from weak algebra skills. This is frustrating because these are students in an honors level Precalculus class who have successfully completed honors level Algebra One and Algebra Two. Perhaps it is because it is "out of context". Which is not a good excuse as it shows me they didn't learn conceptually what it means to solve an equation (and what those algebra skills, such as factoring, are really about).
So I start solving trig equations in the introduction unit on trig. The focus of that chapter really is understanding trig functions and the trig ratios that correspond to various angles (having learned right triangle trig in Geometry & Alg 2).
Then we see solving trig equations again in the Analytic Trig unit - where we also simplify and verifying trig expressions using various identities (and algebra techniques). Later we solve equations in this same unit using more complex sum & difference and multiple angle identities.
This blog post looks at solving trig equations including basic trig identities. We work on these right after we spend a few days on the basic identities (reciprocal, quotient and Pythagorean) and simplifying trig expressions. The important thing for my students is to practice. So many of my ISN pages are examples. I have students do these together in their small groups and we share work in the larger group setting.
I usually introduce this section with a few complicated equations that I ask the small groups to solve. I remind them of what we did last unit and that so far in this unit we have some new tools available to use (those previously mentioned identities - it's a good idea to ask students to share what new tools we have and get feedback from class before they solve). After we do this introduction work (solve, share, discuss). I give them the information sheet for their notebook (see above).
Then we dive into doing examples Some we do together, some we do in small groups. Ten examples in all.
Now this year a student got confused with "solving trig equations" and "evaluating inverse trig functions". They thought they were the same thing and got stuck in thinking about the limited domain & range for inverse functions. I was like "uh-oh" - we discussed that misconception. Then next class I gave them this foldable to summarize our conversation:
Since I had a page opposite that little addition in our ISNs, I gave students another solving example for a warm up for the blank page:
In retrospect, I will save some paper this coming school year by having students do those 10 original examples directly into their notebooks. A composition notebook does have 200 possible pages and this year in PreCalculus we used only 147 pages.
My files on equation solving can be found HERE. These include the two ISN pages and a summary practice sheet of examples.