http://mathforum.org/mbower/johnandbetty/p30/p30.htm
The next lesson after trigonometric form of complex numbers is working with DeMoivre's Theorem. We calculate powers of complex numbers and then from there look at different roots of complex numbers.
Most of my classes start with a Q & A on the last lesson and then a POD quiz (problem of the day quiz) based on the last lesson. Something quick to assess understanding.
I have found that a good way to start this new lesson is to give them a complex number and ask them to square it. (something like -2 - 2i ). Most students can do this pretty well using the distributive property or the box method of multiplying binomials. But then I ask them to raise the same complex number to the 6th power. Since we didn't get to the binomial theorem this year they have no real idea what they could do except keep multiplying. An overwhelming prospect. This sets up some reasonable rationale for today's DeMoivre's theorem. I go through raising it to the 6th power using this new "formula". So much easier!
I use the following foldable and examples in our composition notebooks (ISNs).
DeMoivre's Theorem
Then we switch gears to the inverse - what's the inverse of raising a number to a power? Taking roots. I begin this discussion by asking, "What is the square root of 64?". Being an honors class they easily remember there are two square roots, BOTH 8 & -8. Then I asked what is the cube root of 8? Another easy one, 2. But then I tell my students that there are TWO MORE cube roots. And that the number of roots is always equal to the index "n". However some roots might be in the set of complex numbers.
We look back at example 2 in our last set of examples. The original complex number was raised to the 12th power and the result was 4096. Another 12th root of 4096 is 2. But we started with a complex root in our previous example. We talk about what the other roots look like (there is one more real 12th root in this problem...).
From there we set up our new formula:
Nth Roots of Complex Numbers
We go through an example very carefully. Notice the foldable tapes on the side of this notebook page and when you lift the flap you see the steps we follow. (a note here on taping in foldables - tape it both on top and then lift it and tape it under to secure it well in the notebook).
Students start to notice a pattern in the angles of these roots. I use this opportunity to look at the roots on a unit circle and students see how they are evenly spaced. Cool stuff!
Since this is our last topic for the year we overflowed a bit onto a few more pages....
All my foldable files are found here and a worksheet of this mini unit can be found here.

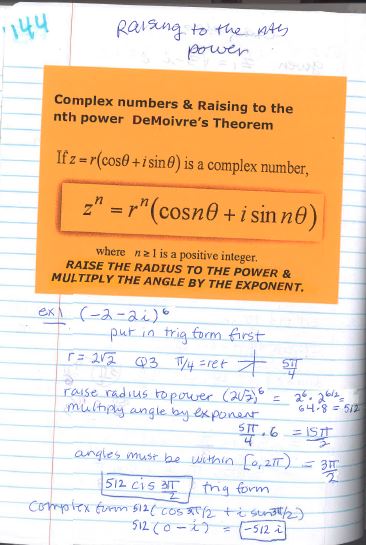






Hi, Im a Physics and Maths teacher carrying out a Maths C subject knowledge course, I have been struggling to get my head around the nth root, finding your blog has helped immensely, the text books I have to go from and the wide range of different methods/steps across the internet have done nothing but confuse me. This is so clear and so simple, Thank you :)
ReplyDelete