https://en.wikipedia.org/wiki/Complex_number
I love starting off my lesson on Trigonometric Form of Complex Numbers.
I start off by drawing a real number line and I talk about the set of real numbers. I even do a mini-review of the sets of numbers that make up the set of real numbers.
https://www.pinterest.com/marlab327/real-numbers/?lp=true
This shouldn't take a lot of time, it's just a quick overview on how cool numbers are and how they relate to each other. I summarize by saying the set of real numbers can be shown graphically with a number line. Very cool, very simple.
http://www.onlinemathlearning.com/real-numbers-gre.html
And how do imaginary numbers relate to all this? Again, quick reminder of why we have imaginary numbers (ever try to take the square root of -1?). Again this is very quick and culminates in us having the set of complex numbers! Tada!
https://www.tes.com/lessons/uIuFvVVAvuMA8g/complex-numbers
So from there I get to show them how the imaginary numbers relate to the real number line with the imaginary axis! I stress that it is not a coordinate plane even though it looks like one.
Now this is something they should have learned in their earlier math courses so it is a quick intro to set the stage for Trig Form of Complex numbers.
From there we compare the three different ways we can write a complex number (with a greater focus on the first two): Standard Form, Trigonometric Form, and Polar Form. We look at them graphically with my first foldable.
Inside the foldable we look at converting back & forth between standard form and trig form.
Students then try out some examples on the page opposite.
Now we have an 82 minute block so I still have time to go over multiplying and dividing complex numbers in trig form. Providing some rationale is a bit challenging since it's pretty straightforward multiplying complex numbers. They know it's like multiplying binomials. Dividing is a little trickier. When the numbers are in trig form there is a nice straightforward method. My foldable shows the official definition/formula on the front.
But inside I do give the "quick" way to do it.
I also allow the shortcut way of writing complex numbers in trig form using CIS.
And on the page opposite we have some examples:
This year, I had to be out the day after this lesson. So I gave the students the above examples as a warm up for that class. They had a POD for converting complex numbers and then worked on a practice sheet of the skills we had gone over in this lesson.




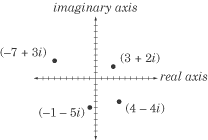





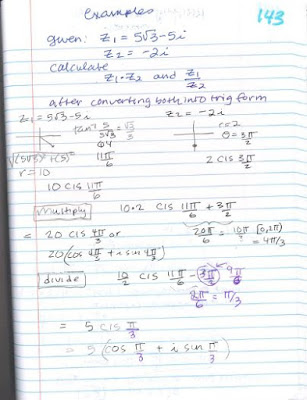
No comments:
Post a Comment