Summer Goes SO Fast!

Ah, it's the end of July. When that comes along I know my summer vacation will end soon. Well, I have three more weeks. And really that last week I'm in & out of school getting my classroom ready. August 24th will be here before I know it.

Be sure you get out and enjoy the summer a bit before it's all over!  Life starts moving very quickly once school starts up again.

Car Comparison Performance Task - Exponential Functions

http://mrec.tv/car/car-comparison.html

Here's a performance task that's a great way to tie in what students know about exponential functions.

Big Idea

Students are given the following task:

Determine if there is a significant difference in value over time for two types of cars by determining and examining their approximate rates of depreciation and using that and other factors to determine which car would be a better value for your needs. 

Setting the Stage

First it's a good idea to brainstorm how students might compare two cars they are interesting in purchasing to determine which is the better deal. Is it enough to compare purchase price? Are there other factors they should be considering? Get a good conversation going, have students list things they should consider on their papers and then share in whole group on the board.

Students have learned about car depreciation in a general way. If they are still uncertain as to what that is you can search on youtube for a possible video to show them. I have students read this article on depreciation. I tell students they are going to compare two types of cars to see which is the better value. They will use depreciation rate as one way of comparing and then choose one other characteristic. We'll have time in class to collect data on the "Kelley Blue Book" site.

Then usually have students then read the article for HW and also read over the performance task details. They are also to think about two types of cars they might want to compare. They might want to compare SUVs and mini-vans. Or two-door sports cars vs 4 door sedans. Or american made vs foreign made. There are a lot of possibilities and encourage them to discuss with their parents about what they think. Students should come in with a general thesis question next class. They do not have to collect data yet or even choose specific makes of cars yet. We'll do that the next class. I also tell students they can work in pairs (this is the ONLY PT they can work together on. I hate having students work together on a graded assignment but every year students beg me to let them do this. And every year there are students who end up doing most of the work for their group who come to me to complain. Sigh. But I figure one PT for them to do together will appease them and it will be less grading for me. I do a big stern talk about being sure you carry your weight if you work in pairs, etc).

Collecting Data

The next class students come in all ready to collect data and start this PT - so we have a computer lab day. Students will collect data on the internet. I have to plan ahead to do this in our school, we don't have many full class sets of computers and I have to be sure to sign up a few weeks ahead of time. Warning - if you have students use ipads to access the site the "tablet" site is a bit different from the general webpage. So be sure you are familiar with what that looks like and how to navigate.

HUGE DISCLAIMER
This can be a little confusing. We really cannot collect true data for calculating depreciation because we can't buy a car and then record its value each year for 5 years. We have about an hour to collect our data. So you have to explain this very clearly and carefully to students so they understand how we are sort of fudging our data but that its still valuable to us even though we aren't truly tracking the value of a single car over time.

What are doing is collecting data on two cars that have been manufactured for at least five years. Students will choose two specific cars, go to Kelley Blue Book (http://www.kbb.com/)  and find the new price of their first car. I strongly recommend that you work through this yourself on the site before you have students do this. My performance task directions are pretty specific but they may redesign their site so things change (and tablet or phone mobile sites look different).

I give students a data collection worksheet to record their data.  They will use tables that look like this:

So the new price goes in for the y-value of "New". Then they look up the price of the same make & model car for the previous year and that goes for the y-value of a 1 year old car (x = 1) and so on with the used car prices. They will use the x values noted in the table when inputting data in their calculator NOT the actual year of the car.

They do this for both cars.

Warning - all sorts of things can happen when students are collecting data. They can find that one of their cars was not manufactured for a given year or that the value is lower for a newer year than an older year. Weird stuff can happen. So you have to think on your feet and decide what they should. Sometimes they have to start over and find another car model.

I know some teachers in my school limit students to a dozen different cars to choose from that the teacher researches ahead of time to be sure the data makes sense for those cars. This is a good idea. I have advanced students so I like them to learn about the quirks and limitations of working with the internet. They are pretty good-natured about having to start over so it has worked out fine for me.

Pulling it All Together

Now students have collected data and they have information about two cars. They need to create a nice table of all their data and get pictures of each of their cars. They should have something like this:

Then they have to apply the algebra they've learned, collect some more information about their cars and pull it all together to make a comparison. See the performance task details to see very specifically what they are doing.

The next class I like to talk briefly about what they do next. They need to have some sort of presentation of their results. They can turn it in as a powerpoint, as a booklet or as a poster. They do not have to present in class. Sometimes I get a pair of students who wants to present their powerpoint and I give them the opportunity as long as they can do it in ten minutes or less. But generally students want to just turn it in. It's a great idea for them to present their results but I'm always am working with time constraints - so much to cover, so little time. Anyhow, I show students this PowerPoint that gives a "sample presentation". I won't post this on line for students to refer to because I want them to have things in their own words but I like them to have a good idea of what makes a good and complete presentation. I don't give students any more class time to complete this task. They have about a week to turn in their final work. 

How I grade this

I have a teacher rubric with details on how I grade this. Feel free to contact me for this and I will send it out to you.

Skittles Exponential Lab

Explore a real-life situation of growth & decay, simulated with M&Ms.

I like to do this lab just as we are first learning about exponential functions. It's a great lesson to do on a half day PD day or just before a long weekend/vacation or on a Friday.

There is some expense involved (don't all us teachers spend our own money supplying items for our classroom? There's always something we need for a lesson or to enrich our classroom environment that we are spending our own money on).

Supplies needed:

A large quantity of skittles (I buy the "warehouse" size bag that you can get at a place like BJs or Sam's club. Amazon sells them too). I used to use M&Ms but skittles are better overall, you avoid any issue with allergies.
Paper cups (small ones are good - 6 ounce?)
Paper towels or large paper plates (or have students create a workplace* with a piece of paper).
Hand sanitizer (or have students wash hand before handling the food)
optional - small ziploc bags (for students who want to take leftover skittles with them)

*you can create a "workplace" for the skittles with an 8.5x11 sheet of paper. Just fold a small margin over on all four sides, then open it up a bit. It creates a workplace where they can empty our their skittles cup without the skittles going all over the place (like the floor!).

Additional Prep Work

For each group of students prepare the materials. Put two cups together and inside the cup put a generous handful of skittles (probably about 100, but I don't count them!). As for group size, I have the usually work in pairs or groups of 3. If you have too many people you'll have someone who isn't doing anything and you don't want anyone being idle when there is candy all around the room.

Starting the Lab

• Have the students get in their groups if they aren't already situated that way
• Hand out the lab information sheet and have students read it over. Discuss fish ponds and why populations grow or die off. Usually there are some students who fish in class and you can briefly discuss how ponds are "supplied" with fish just prior to fishing season.
• Hand out the supplies (cups with skittles, paper plate or paper towel or create the "workplace" noted above).

General Lab procedure

• Trial One - Growing Population - students need to follow the directions on the lab information sheet (they DO NOT eat the skittles, they are needed for the next trial). They collect their data. They may not get enough data to fill in the whole table - that's okay, just fill in enough until they have no more skittles (the last toss will tell them to add a certain number of skittles that they do not have - just tell them to calculate the total they should have and record that. Then they are done with trial one.
• Students can wait and do all the graphing calculator work after they collect their data, so they move on to...
• Trial Two - A Dying Pond - again students are following the directions on the lab information sheet and they may not use the whole table for data collection as in the first trial. They just collect data until they end up with one or zero fish. 
• Once all the data is collected, students can eat their skittles. They should be doing work when they snack!
• Students do the graphing calculator portion of the lab - creating scatter plots of the data for each trial. If you haven't done so already talk about doing regression on the graphing calculator and how for exponential it will calculate "a" and "b" values for students. They should round "a" to the nearest whole number and "b" to the nearest tenth. 

Examining the Results

Have students write results on the board. I write two headings

• GROWING POPULATION
• DYING POND

Students write their equations under the headings - there may be a bit of variety but there will be similarities that come out.  First the Growing Population will have a base very close to "2". And the Dying Pond will have a base very close to 1/2. The "a" values will vary, but for Growth it should be close to "2" (represents starting with two fish initially, the mommy & daddy fish) and for Decay it will be close to the total number of skittles they started with. 

Wrapping things up

der Now you can have a discussion of what those equations mean and this whole new type of function we'll be studying. You can have the students do an ISN insert summarizing or defining exponential functions or defining growth & decay. I haven't decided how I'm going to use my ISN in summarizing yet. My student teacher did this lab in class this past year. She actually used an ISN insert to drive the lab. I still like my lab sheets and think I just want my ISN insert to summarize.

Here are her ISN inserts:

Algebra One Unit 7 Exponential Functions

Now we get into the fun stuff!  Applications....

I like to start off by considering a new type of function. A fun way to do this is with a skittles lab (or M&Ms) which I'll detail in my next blog post.

From there we define in a general way exponential functions and then compare linear and exponential functions. We look at the difference between growth & decay. Then we explore additional applications by looking at Half Life, Compounding Interest and Logistic Functions. Also we do some regression analysis of exponential data.

I'm not going to go into a lot of detail on these now as my student teacher covered these topics in 2014-2015 school year. But I will do an update in spring 2016 after I teach it and tweak all my ISN inserts.

For now, here are the inserts my wonderful student teacher used.

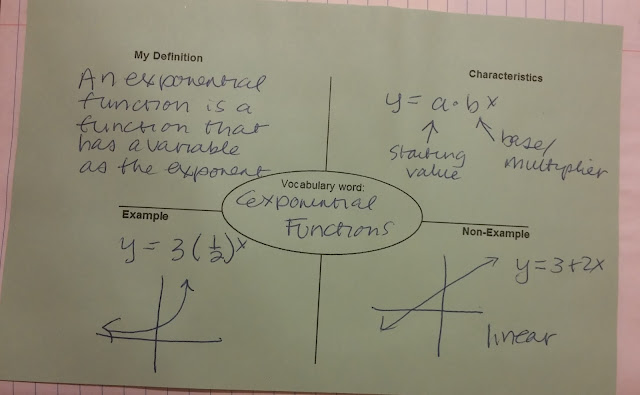
 Regression Analysis pages:

first a reminder of how to use the graphing calculator

 then an example:

 Other Applications:

Space was limited in this foldable so next year I'm thinking of creating two two page foldables for these four topics.

Here are the ISN masters for these topics.

Here are some worksheets and lesson materials I used for these topics.

Algebra One Unit 7 Properties of Exponents

After our introduction day of laying the groundwork we get into all the properties. Since my students have seen this material before we can take one of two approaches. I have to gauge how strong a group I have each year. I think they will continually get stronger and I will eventually be able to do option two for everyone. Remember I have an advanced class so this will be easier to do.

Option One - work through each property

Develop each property with students. I like doing discovery work on this. But I also find that students "remember" the rules but can't justify why they work. So I may "tweak" my discovery sheet to be clearer about justifying results. After going through each property then proceed into option two.

Option Two - Students do around the room activity to gather examples for properties.

So they know the properties and now can they identify examples that illustrate each? They are given a summary of properties worksheet to find examples for and fill them in. Examples are taped around the room. They can work together. Teacher is walking around with a master key to assist students only if absolutely necessary (and be stingy with the help - ask questions of them back or say hmmm... that doesn't look like that should go there). I tell students how many examples they are finding for each. See the master key for the examples. I write them on half page sheets of paper and tape them around the room. Students have to simplify each as well.

Other useful practice for students:
A Puzzle Partners worksheet
An All Properties worksheet with lots of examples and the answer key.

And there is an ISN insert too that students put into their notebooks. my student teacher did these inserts, she did a great job, but I'll probably do some tweaking so will post my new items in 2016 as I do them.

*did I tell you what cool handwriting my student teacher has?

Powers and Negatives can be a tricky combination, so we made an ISN summary sheet for that (found it on pinterest and the blog domain page has expired but it was called somebecomepearls.com).

and it appears that I forgot to take a picture of the inside three doors - so this is from pinterst:

Other useful practice for students:
A Puzzle Partners worksheet
An All Properties worksheet with lots of examples and the answer key.

Of course after this I do give my students a summative assessment (quiz).  After the quiz they take this little handout and then we talk about radicals - squares and square roots once everyone is finished with the quiz.

We go through the first 15 perfect squares and their square roots. We also talk about other roots too and list the first 5 perfect cubes and their cube roots. All students should memorize those perfect squares and cubes - they are all good number facts to have easy mental access to. I usually do a quick memorization quiz early on for this. (yes there are some things that just need to be memorized).

To support this radical work, I want an ISN insert on radicals.  this is not in my notebook but I want to use it in the 2015-2016 school year. Thank you again Sarah Hagan from math=love  (I think I'll make the first page a "booklet" so inside students can write the perfect squares and cubes they have to memorize.)

Then we get into rational exponents - this can get kind of tricky to develop and not just "tell".  Here are some rough notes of what I do in general after the quiz on regular exponent properties and leading into rational exponents.

Then there is an ISN insert

We had students convert back and forth between radical and exponential notation.

Then we had students apply the properties of exponents to rational exponents. Here are some worksheets that I used. 

Here are my ISN masters.  I can't find the master for squaring a negative, so I will double check with my student teacher and post it once I find it OR make another one.

Unit 7 Laying the ground work for Properties of Exponents

When we were first starting our curriculum writing for unit 7 we were once again horrified to see that students start with properties of rational exponents. This is in Algebra One. I've always taught the initial properties of exponents with integer exponents. I guess students will now learn this in sixth grade so that by ninth grade they are all set and we can go write into fractional exponents. But my students are very far from that reality (especially since our first common core year in Algebra One was also the first year they did common core in 6th grade in our school system). Yes, students see the properties in Pre-Algebra (8th grade) but have no understanding of where they come from, they just remember there were some rules they memorized.

So back to square one.

I'm a big fan of develop the knowledge, don't memorize rules. That way you can recreate something you may have forgotten the details for as long as you can remember the basics and develop knowledge. My high school years (in the 70s) were spent memorizing formulas and being discouraged from asking why. Very frustrating! So as a high school mathematics teacher I feel it's important to develop those whys.

This blog post is on a discussion day that I have with students in reviewing some properties of mathematics and reminding students of the awesome power of ONE!  (who would think ONE would be such a powerful number!).

After the unit test from the previous unit - I jumpstart thinking with this exponents vocabulary puzzle sheet. They complete that for homework.

Then I have students do this worksheet as a warm up - all problems they should be able to do from their previous experience with exponents.

So now we are ready for our discussion class. After going over the warm up I refer to the following (written on the board):

·          1)  Definition of Exponentiation

·           2)  Commutative Property

·         3) Associative Property

·         4) Identity Property of Multiplication

·          5) What's behind the process of simplifying fractions (or why "cancel" is a dirty word)

    We talk about what each of these mean. Here's a basic "script" of how our discussions go (I typed it all up one year to have a hard copy). I don't just talk through all these things, I ask lots of leading questions and ask students to give me examples. They should know all this material, they just need a kick start to remember.

  1) Definition of Exponentiation

The exponent of a number says how many times to use the number in a multiplication.

In 8² the "2" says to use 8 twice in a multiplication,
so 8² = 8 × 8 = 64

Some more examples:

Example: 5³ = 5 × 5 × 5 = 125

• In words: 5³ could be called "5 to the third power", "5 to the power 3" or simply "5 cubed"

Example: x⁴ = x · x · x · x

• In words: 2⁴ could be called "2 to the fourth power" or "2 to the power 4" or simply "2 to the 4th"

So, in general:

an tells you to multiply a by itself, so there are n of those a's:
2) Commutative Property The word "commutative" comes from "commute" or "move around", so the Commutative Property is the one that refers to moving stuff around. For addition, the rule is "a + b = b + a"; in numbers, this means 2 + 3 = 3 + 2. For multiplication, the rule is "ab = ba"; in numbers, this means 2×3 = 3×2.   3) Associative Property The word "associative" comes from "associate" or "group";the Associative Property is the rule that refers to grouping. For addition, the rule is "a + (b + c) = (a + b) + c"; in numbers, this means 2 + (3 + 4) = (2 + 3) + 4. For multiplication, the rule is "a(bc) = (ab)c"; in numbers, this means 2(3×4) = (2×3)4.                            4) Identity Property of Multiplication The identity property of multiplication, also called the multiplication property of one says that the value of a number does not change when that number is multiplied by 1. Copyright 5) What’s behind the process of simplifying fractions…(and why you can’t “cancel” when it’s addition) What allows you to simplify fractions? A somewhat extreme meme to emphasize the horror of this type of mistake..... http://mathcurmudgeon.blogspot.com/2014/01/do-this-and-bunny-dies.html  And I wrap things up by having students do this worksheet for homework.

Systems of Equations Project - Business Letters

This is not really a performance task (which is what we are trying to do one per unit in Algebra One), it's more of a project. But it's interdisciplinary, gets students to apply math in a real life situation, easy to differentiate and really great! The other Algebra One teachers in my school created a performance task for 2013-2014 and although it was okay they went back and used this again in 2014-2015.

Overall the "problem" is not so hard for students. The tricky part is communication and attention to detail. Two not so strong skills for high school students! But it's also fun for students because it has role playing and some creativity. And if you have students who are far better in English than in math, then this is their time to shine!

The Premise

Students are given a letter from a business that contains a problem that can be solved using a system of equations. They take on the role of the business person who received the letter. They solve the problem and write a letter back to the business clearly communicating the solution including an attachment with all the algebra details. Here is a sample letter that a student might receive:

Teacher Prep

I have a whole bunch of letters at varying levels of difficulty. Prior to handing out the student letters I determine who should get what letter (here is the differentiation) with my advanced class all receiving a more complicated problem (mixture). I personalize the letters, typing each student's name where it says "your name". And then I print them all out on the only color copy machine in the school. Since I want a really nice polished letter back from the students I think it's important that what I give them is full color. 

The Process

Students receive their letters in class. They are given general instructions on what their task is. With an average level class I then have them solve the problem at home and come in the next day with their solution. As students are doing class/group work on some other task I go around the room and check their solution. You could also collect them and hand them back the next day after checking.

I then go over the whole business letter concept. Stressing that they are playing a role and need to be professional. They are not writing this letter to a friend (so they should not have pleasantries such as "how are you doing?" in the letter). Spelling and grammar should be perfect, they want to make a good impression. 

A tricky bit for students is understanding the whole address placement and general format of greeting and closure. For example the letter above has the address header for"Gourmet Boutique" and they need to understand that that address now goes under the date in the place of "Coffee Distributors". Basically the two addresses switch places. I point out that they should have the same format with the address blocks, the date, the salutation ("dear....the person who wrote them the letter they got - but don't include their title here) and the closure ("sincerely....their name and title - they make up a title).

The creativity comes in now with a cool header with a fun typeface and a graphic at the end of the letter.

Another formatting comment - the letter is single spaced and in English classes they are used to doing essays in double space.

After we go over the general formatting I talk about content. They should see that a letter has a general format in its paragraphs.

There should be three paragraphs in their letter. 

The first paragraph has a professional greeting of some sort and restates the problem that the student received. They can lay on the schmooze pretty thick because they are wooing a client. (I am honored that you have chosen Coffee Distributors for your coffee needs. I am sorry that I was not clear on the correct mixture quantities for your premium South American blend. I am happy to provide the details regarding the exact quantities of Brazilian coffee and Colombian for your personalized blend.) I would not write out a correct first paragraph but would definitely "say" it for students so they can hear how it might sound. Students are told that this paragraph is similar to an introduction sentence in an English class essay. 

The second paragraph is the "meat" of their letter. Here they state the question (again!) and communicate the answer. They comment on how they solved it in a general way with a reference to the attachment. (This result was calculated by using an algebraic system of equations, see the attachment for full details and mathematical explanation). 

The third paragraph just wraps things up - there are professional pleasantries, possibly a direct reference to the problem and reassurances that if they have any other questions they just need to ask. 

(Thank you again for your interest in working with Coffee Distributors. I assure you that we have only the highest quality product and our blends are extremely well rated. If you have any additional questions please do not hesitate to contact me. Thank you again, and we look forward to working with you in supplying all your coffee needs.)

Sadly, in general, I find that students are not especially good writers. And this professional business letter format is so foreign to them. So it's important to stress that they are not writing an email or a text to a friend. They are trying to grow their business and develop trust and respect. So they must be very professional and have impeccable spelling and grammar. One error could lose a client for them. 

I also talk about the attachment. This shows all the "algebra details". It should not just be work, it needs to have some words explaining the set up and implementation of their method. I am looking for the variables being defined. the system of equations clearly shown with some rationale for where it came from. The method used in solving should be stated (the linear combination method was used to solve this system). When the value of a variable is found state clearly what that represents. A short explanation of finding the other variable (that value is substituted into either original equation and then the other unknown is solved for). There should also be a full sentence stating the solution with respect to the problem originally posed. (you will need 80 pounds of the Brazilian coffee and 120 pound of the Colombian coffee). 

With all that in mind, I would have all the students in my average classes do a rough draft (of both the letter and the attachment). In the past I've had students work together on some peer editing. This sounds all wonderful and cooperative and collaborative. But I hate to say this, I find peer editing to be a waste of time. Their peers are going to say that their letter sounds great. They often do not see grammatical errors and don't recognize if something sounds unprofessional. So I would usually collect the rough drafts, make general comments on them and hand them back. If a rough draft letter needs a lot of work I make the general comments but then urge the student to come for one-on-one help. 

I've been working with advanced students for the last few years and the peer editing can be productive with them. They should work with a checklist when editting. And have a short amount of time (10-15 minutes). And I offer to those classes if they want direct teacher input on their rough draft to come during my extra help times and I will work with them. 

Then students have the final task of creating their letter and their attachment.  The final version of the letter must be typed and have an interesting header and a graphic/picture. The attachment does not need to be typed. I give them a few more days to get this completed and turned in.

Resources

Here are all my materials for this project:

General Information and Rubric

Peer Editting Checklist

Sample editted letter

How to format attachment

Regular (easy- medium) difficulty problems

Advanced (mixture) difficulty problems

Acknowledgment

Where does this project come from? I don't think I have ever had a truly original idea. Everything comes from something I've read or seen elsewhere. This project resulted from my experience in a session at an NCTM or ATOMIC convention in the 1980s. It was a very similar project but not so detailed and all the letters are mine.

Introducing Systems of Equations - Exploring Scenarios

http://www.thedogtrainingsecret.com/blog/teaching-dog-tolerate-love-children/ 

I always like to start a new unit with some understanding of why this might be useful and what the underlying idea is for the concept. What really is a system of equations? What does it represent?

Well a system of equations is usually defined as: A system of equations is a collection of two or more equations with a same set of unknowns. (SOS math)

What does that mean? How do we start exploring that? Dan Meyer has an interesting blog post (dy/dan) on this from February 2014 

[Fake World] Culture Beats Curriculum

I recommend reading it and considering how it fits into how you introduce systems. I like his approach and I also like to look at some scenarios that later we will describe algebraically with systems of equations. But right now we just consider them and try solving them without algebra (draw a picture, act it out, educated guess & check, make a table). 

Consider the classic "kids and dogs" problem: 

 In the park one day, I saw a bunch of kids and dogs.  Counting heads, I got twenty-two.  Counting legs, I got sixty-eight.  How many kids were in the park?  

(I bet you are trying to write a system to solve this right now aren't you? stop!!)

You can actually solve this by drawing a picture or more dramatically by acting it out. I saw this years ago in an issue of Mathematics Teacher (NCTM) but do not have the reference to it now. It's so so cool and can be done with younger kids. If you are going to act it out create a problem with less heads because that number of students will have to stand in front of the class.

Drawing a Picture

To draw a picture you draw twenty-two heads. And since you know that both kids and dogs have at least two legs per creature, draw in two legs for each. (I have students do this on the white board - one draws all the heads, then someone fills in the two pairs of legs each). 

How many legs have we drawn so far? 44 legs

How many legs did you originally count? 68

So what does that mean? (there are 24 more legs that we are not seeing yet in our drawing)

Someone will come up with that we have to draw those other legs on our creatures - doing two per creature until we use up all those 24 extra legs. (12 pairs)

Visually we see 12 creature with 4 legs (dogs) and 10 creatures with 2 legs (kids).

Students love this by the way - it is fun.

Acting It Out
You have the total number of heads acted out by that many students. So with this problem you have 22 students stand in front of the class (really a good idea to scale this down to a smaller number of heads for acting out). Now tell them that some of them are kids and some of them are dogs. But we'll start by saying that all of them will raise their arms (or front legs) in the air. Then we ask rest of the class - how many legs do you see on the ground? (44) But how many legs did we originally count? (68) So how many of those front limbs in the air are actually dog legs? (24) and how many pairs of front legs does a dog have? (2) so 24 legs is how many dogs? (12 dogs!) and from there you can calculate the number of kids (10).

This is a lot of fun too, just hard to do individually or at home. But it's a good way to introduce this and then show them the draw a picture method.

Now students get stuck on wanting to draw a picture but I want them to experience other methods too. You'll find in the next two methods students will really really want to start writing algebraic expressions and equations. I avoid doing much of that, however some little expressions for the conditions can be useful for some of the trickier conditions. But don't do any equations yet!

Educated Guess & Check
Guess and check seems so "random". But with educated guess and check students consider the result of a guess and then adjust in their next guess if the first guess is wrong. Making a table to organie their guesses is a good idea too. Have students consider this problem: 
The sum of Freida & Gene’s ages is 21. Freida’s age is 3 less than twice Gene’s age. How old are both Freida and Gene?
 After some discussion show students how to set up an organized guess & check table with four columns – Freida’s age, Gene’s age, check condition #1, check condition #2. Describe in words, do not get into writing equations (that’s a future lesson). Use the conditions to guess & check, continue until solution is found.

Make a Table

Now you might think - hey they made a table in the above problem. But that was just to organize their guesses. This table is to keep track of a pattern and look for a common result for two items. Consider this plant growth problem:

Plant A and Plant B are on different watering schedules. This affects their rate of growth. You will compare the growth of the two plants to determine when their heights will be the same.

Plant A starts at 5 inches tall and grows 2 inches per week.

Plant B starts at 2 inches tall and grows 3 inches per week.

When are the two plants the same height?

We can start by deciding what the independent and dependent variables are (IV # of weeks, DV total height of plant in inches). And then we can make a set of tables to keep track of the plant growth for each over a number of weeks.

After filling in the tables students can see a common set of values.

Be sure students can articulate what that ordered pair (3, 11) represents!

From these examples I then give them a practice worksheet of problems to work on in their small groups and to complete for homework.

Unit 6 Systems of Equations

The next few blog posts will not be as detailed because at this point in the school year I had a student teacher. So I am going to post her ISN work with some commentary. But after I teach these units (February - May 2016) I will update with my own materials and more detail. I don't think I have a student teacher this coming school year. (And my student teacher this past year was very good! What a trooper working with interactive student notebooks and creating her own materials! She did a great job and she has beautiful handwriting). 

Exploring Scenarios

Systems of Equations - we take a little different approach with starting this unit. We don't jump right into "here is a system and here is how we solve it". When planning I like to think about "what is a system good for? why does it exist as an algebraic process?". So we start off with "Exploring Scenarios" to get an idea of what it means to have two unknowns and two conditions. I'll do a separate blog post on that because I think it's a really valuable way to begin, for students to develop some overall understanding. We didn't have anything in our ISN on this but I will this coming school year.

ISN Foldables

One comment on coordinating your ISN with a student teacher. Let them put their inserts in your teacher notebook. I started off by giving my student teacher her own notebook to put her foldables in and I tried to keep up with her. But I wasn't always in the classroom when she taught so there were gaps. When she took over my lower level Algebra One she did use my notebook and it worked out so much better.

This was a cute idea for demonstrating substitution but I'm not sure if it's that useful in the ISN. I also came across the "blob" method for an insert on substitution method and used that with my lower level classes.

Cool summary foldable but the space got tight for showing work clearly. I like to have a lot of space.

Love the examples (go on right hand reflect pages)

My student teacher did a great introduction activity for mixture problems with Kix and CocoPuffs cereal. I'll have to post that when I use it. She had this foldable to show the table method for mixture problems. I've never been a fan of this because you have to remember how to set up the table and that can get confusing. I won't use this next year but someone might find it useful so I'm including it.

Really nice summary bit here - lots of time consuming cutting though, I'd suggest giving it to students the day before and they have to cut for homework. This would be left hand learning and then I'd include some algebraic examples for them to solve on the "right hand reflect" page.

Some good stuff here for systems of linear inequalities. I just was not in class for most of this and some things are blank and we've got an extra blank page. So this needs some reworking.

 Oh, in general I'm not a fan of all that text with "fill in the blanks". There is not a lot of space for filling in and I think when we give the students so many words they mechanically fill in the blanks without thinking about what it means.

And here is the folder with all my student teacher's foldables. 

In the Future....

Next year my tentative foldable plan for this unit is ...(L is for left side learning, R is for right side reflection).

L Exploring Scenarios  R example for warm up

L Systems of Equations defined, what a solution is, checking solutions R examples

L Solve by Graphing  R application example

L solve by substitution R application example

L solve by linear combination  R application example

L mixture problems  R example

L Types of Solutions  R algebraic examples

L systems of Linear inequalities  R examples

L systems of linear inequalities applications  R examples 

http://bakerradiologists.weebly.com/2/post/2013/12/calculate-the-rate-of-change-for-the-yellow-cab-calculate-the-rate-of-change-for-the-blue-cab.html